Vetores

Determinado por um segmento orientado AB, vetor é o conjunto de todos os segmentos orientados equipolentes a AB. 

Um mesmo vetor é determinado por uma infinidade de segmentos orientados, chamados representantes desse vetor, os quais são todos equipolentes entre si. Assim, um segmento determina um conjunto que é o vetor, e qualquer um destes representantes determina o mesmo vetor. Usando um pouco mais nossa capacidade de abstração, se considerarmos todos os infinitos segmentos orientados de origem comum, estaremos caracterizando, através de representantes, a totalidade dos vetores do espaço. Ora, cada um destes segmentos é um representante de um só vetor. Consequentemente, todos os vetores se acham representados naquele conjunto que imaginamos.

As características de um vetor são as mesmas de qualquer um de seus representantes, isto é: o módulo, a direção e o sentido do vetor são os mesmos para qualquer um de seus representantes.

Soma de Vetores

Observação: Embora seja possível definir espaços vetoriais complexos (onde os escalares são números complexos), serão estudados em nossos posts apenas espaços vetoriais reais, onde os escalares são números reais. 

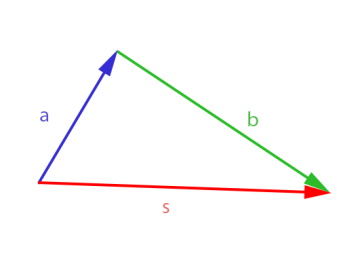
Consideremos uma formiga que se moveu de a até b e, em seguida, de b até c. Seu deslocamento pode ser representado com apenas dois vetores, um seguido do outro. Mas, para simplificar, podemos representar seu deslocamento total de uma outra maneira, com um único vetor s, denominado vetor soma ou vetor resultante.

Consideremos aqui s o vetor soma de a e b. Logo, a + b = s.

Diferente da soma algébrica comum, na soma de vetores o módulo e orientação também estão envolvidos na operação. Existem duas formas diferentes para realização da soma de vetores, elas são conhecidas como regra do polígono e regra do paralelogramo. Vejamos como utilizá-las:

Regra do Polígono

Se trata de um método simples para efetuar a adição de vetores e está representado na imagem acima. Tendo dois vetores não-nulos, devemos desenhar o a no ângulo apropriado e o b, também no ângulo correto, com sua origem na extremidade de a. O vetor soma seria o vetor que liga a origem de um dos vetores a extremidade do outro. No caso da imagem o vetor soma é s.

A lei de comutatividade e associatividade são válidas para a soma entre vetores. Ou seja, a ordem em que os vetores são somados é irrelevante. Logo, a + b = b + a. Quando existem mais de dois vetores, podemos colocá-los em qualquer ordem para somá-los.

Vejamos esse segundo exemplo. Temos aqui dois vetores, u e v:

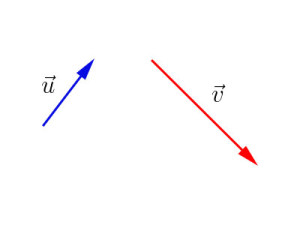
Ao somá-los, obtemos o seguinte vetor soma:

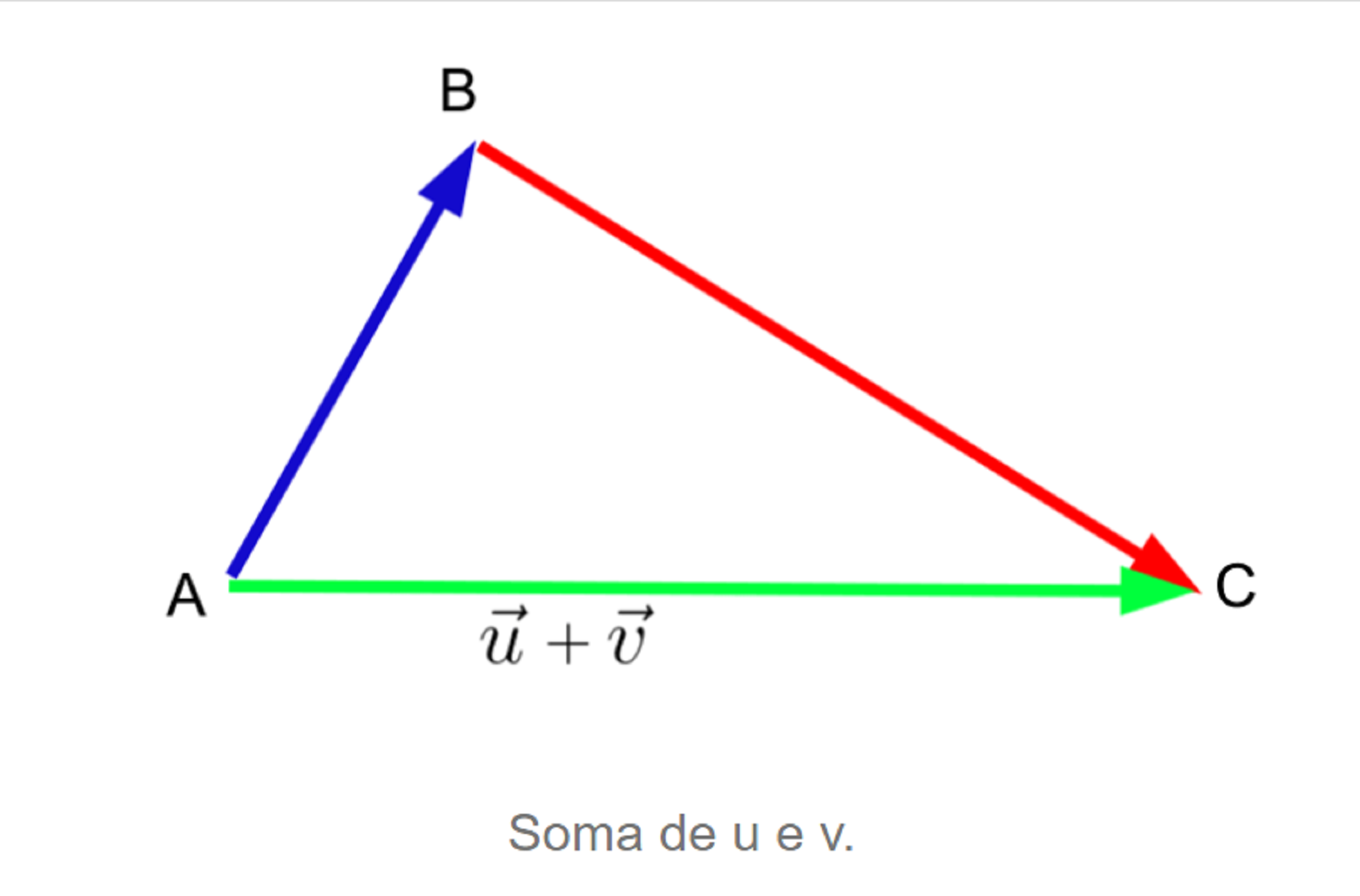
Ou seja, posicionamos a extremidade de u junto a origem de v e como vetor resultante temos u + v.

Regra do Paralelogramo

Sejam u e v dois vetores, ao somá-los, para determinarmos o módulo, sentido e direção do vetor resultante, devemos desenhar o paralelogramo definido por eles. Vejamos um exemplo com os vetores u e v:

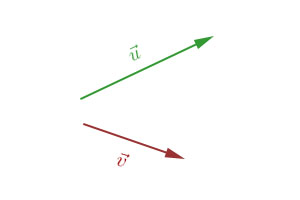
Fazendo uso da regra do paralelogramo chegamos ao seguinte resultado: 

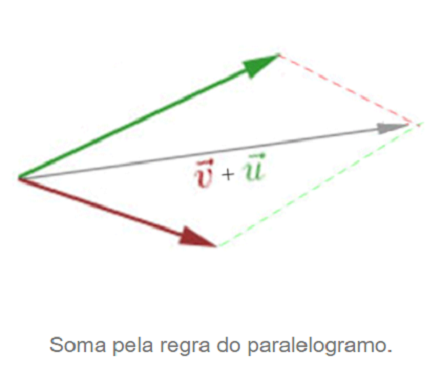
Traçamos retas paralelas aos vetores e ligamos uma a outra. Logo em seguida, desenhamos uma reta "no centro" do paralelogramo, obtendo, assim, o vetor resultante (u + v).

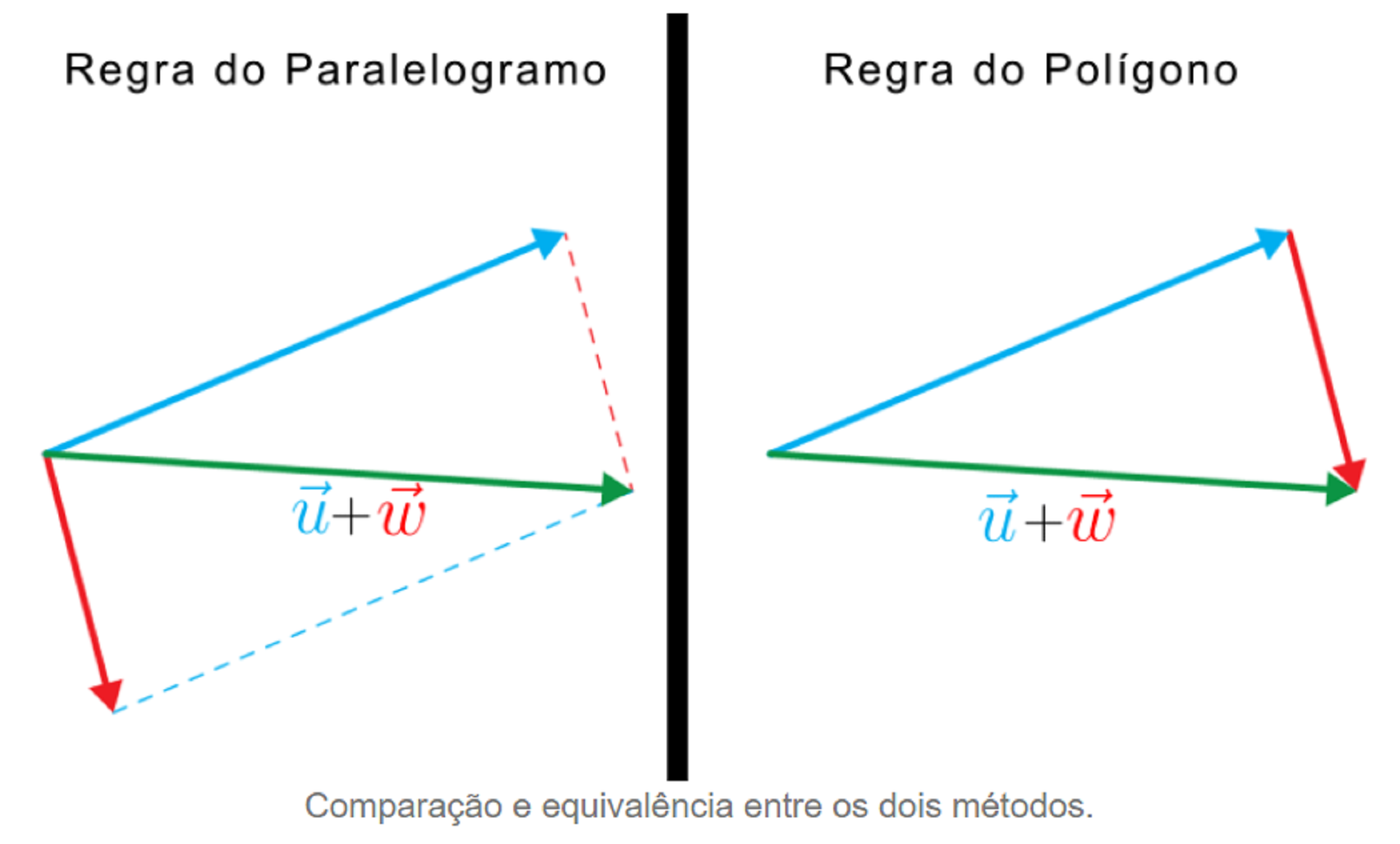
Através da imagem abaixo podemos ver que, independente da regra usada (polígono ou paralelogramo), o resultado será sempre o mesmo:

Para verificar seus conhecimentos sobre soma de vetores, acesse ao seguinte link: